Especial Febrero 2011: Lógica de Raymond Smullyan
LA LÓGICA. Es la forma correcta de llegar a la respuesta equivocada pero sintiéndote contento contigo mismo.
Problemas de lógica
A continuación vamos a mostrar fragmentos de los libros que hemos leído, y otros que hemos encontrado por Internet, para ver las conclusiones que podemos sacar de ellos, para aprender más sobre matemáticas y lógica, y de paso, pasar un rato ameno y divertido ¿Os apuntáis?
Mostramos, primeramente, una frase de las que más veces nos ha dado que pensar, un problema típico que a muchos les sonará de la filosofía que se daba en el bachiller, es la conocida paradoja del mentiroso.
Problemas autorreferentes
Si digo “Yo miento siempre” ¿digo la verdad en ese caso? Si estoy diciendo la verdad entonces no es cierto lo que digo ¿qué paradoja no?
Esto es totalmente cierto, pero en qué quedamos ¿miento o digo la verdad?¿digo la verdad o miento? Este tipo de problemas se denominan autorreferentes, ya que en el propio enunciado se dicen varias cosas a la vez que no sabes cuál de ellas tomar como buena. Es imposible saberlo.
Siempre nos han impresionado mucho las consecuencias de los enunciados autorreferentes, ya que como hemos indicado antes, no sabes a ciencia cierta la verdad que se haya en el enunciado, si es que la hay...
Una solución propuesta es prohibir que un lenguaje hable de sí mismo. Cuando hablamos de un lenguaje siempre debemos hacerlo en un metalenguaje (que es un lenguaje de segundo nivel). Esto les sonará a los informáticos de alguna asignatura.
Un lenguaje nunca puede hablar de su propia verdad. De ese modo no se podrán producir las paradojas que nacen de confundir los dos niveles de lenguaje. La solución es buena pero no vale para la vida común y el lenguaje natural. Mostramos un ejemplo para ver esto con mayor claridad:
En estos últimos tiempos que corren está de moda decir que al ser humano no le importa la verdad y que lo que busca es, simplemente, sobrevivir. Esto, que es una idea muy de moda y que habréis oído por ahí, lo dicen mucho los científicos que estudian al ser humano tratándolo como un animal más que es.
No se dan o no quieren darse cuenta de que su enunciado es autoreferente. Es decir: Esa verdad que enuncian ¿es cierta o es sólo lo que al ser humano le interesa sostener ahora para sobrevivir?
Vamos a ver, el ser humano, al fin y al cabo, hace la ciencia y la ciencia pretende contarnos como son las cosas de verdad. La pregunta surge fácilmente. Las teorías científicas que los científicos desarrollan sobre el ser humano ¿aspiran a ser verdaderas o son sólo “verdades” pragmáticas que van a ayudarnos a sobrevivir como especie? Porque si es esto último que nos lo digan.
Lógica coactiva
Vamos ahora a mostrar un pequeño caso, muy curioso, de un tipo de lógica, la lógica coactiva. Se llama así porque es una lógica que hace actuar al usuario en contra de su propia voluntad, es decir, , dependiendo de cómo se diga lo que se quiere decir o cómo se use dicho lenguaje para explicarlo, puede verse forzado a hacer cosas contrarias a lo que el desea y contrarios a sus intereses, pudiendo llegar si a perder todo lo que posea. Ponemos un ejemplo para que veais este tipo de lógica.
Vamos a explicar este tipo de lógica poniendo un ejemplo del autor del que hablamos y que nos ha sorprendido mucho para explicar este tipo de lógica. Como vereis da que pensar este ejemplo:
<<Cuenta Raymond que durante años, como profesor de lógica, acostumbraba a mostrar en clase a los alumnos una moneda de dólar y un billete de 100 dólares. Entonces pedía a un alumno cualquiera que formulase una proposición. En el caso de que la proposición fuese verdadera, Smullyan prometía darle al alumno la moneda o el billete, indistintamente. (En realidad, su intención en este caso era dar siempre únicamente la moneda, y eso a regañadientes.) Si la proposición resultaba ser falsa, el profesor no entregaba ninguna de las dos cantidades, como es natural.
Pese a su impresionante inteligencia y su enorme sabiduría lógica, a este eminente profesor le llevó algún tiempo, según confiesa él mismo, caer en la cuenta de que existía una proposición “coactiva” que podía forzarle a entregar “siempre” el billete de 100 $. Tal proposición es la siguiente: “Usted no me entregará la moneda.”
Imaginemos, en efecto, lo que podía hacer entonces Raymond:
1. No dar nada al alumno. Es decir, no darle tampoco la moneda. Pero entonces, la proposición del alumno demostraba ser verdadera, lo cual obligaba al profesor, según su compromiso, a entregarle algún dinerillo: bien la moneda, bien el billete de 100 $.
2. Como es obvio, Smullyan, que no es tonto, optaba en primera intención por entregar al alumno la moneda de dólar. Pero eso no podía hacerlo, pues entonces habría resultado que el alumno había mentido al decir “Usted no me entregará la moneda”. De modo que:
3. ¡El bueno de Raymond se veía forzado finalmente, con gran dolor de su corazón, a entregar al alumno el billete de 100 $!
Pero, es que eso no era lo peor del negocio. Lo peor habría podido ser (y lo habría sido si Raymond no hubiese caído a tiempo en la cuenta) ¡Que un alumno suficientemente avispado habría podido sacarle cualquier cantidad de dólares que le hubiese apetecido! Por ejemplo: ¡cien mil, un millón, diez millones de dólares! ¡El gran lógico norteamericano se habría convertido en un muerto de hambre por el resto de sus días, y ello a causa de su poca cabeza! He aquí la fórmula coactiva mágica que habría obligado a Raymond Smullyan a arruinarse y vivir dentro de un barril bajo un puente, siendo el más pobre de los pobres: “Usted no me entregará ni la moneda, ni el billete de 100 $, ni tampoco diez millones de dólares.”
Haciendo un razonamiento similar al de los tres puntos anteriores, se comprueba que, efectivamente, el magnífico profesor estuvo al borde de caer en la indigencia o mendicidad más absoluta. Menos mal que, en un momento de distracción, se puso a pensar un poco, vio el terrible peligro y retiró urgente y definitivamente de sus clases esos enojosos>>(Lemuel, 2007).
Después de comentar la lógica coactiva, vamos a pasar a mostrar acertijos que nos han parecido más divertidos y que llevan un tiempo en pensar su solución. Interesantes para alumnos, profesores y persona que se tercie. Os prometemos que no son difíciles y que os harán pasar un rato divertido. Los habrá fáciles y fácilmente deducibles y también ponemos alguno más difícil que os harán pensar.
Los 4 misterios
Pasamos a ver cuatro misterios que plantea Raymond Smullyan para ver la capacidad de lógica y deducción que puede tener el lector de los mismos.
Primer misterio: Alicia y el día de la semana
Alicia, tras atravesar el espejo, se encuentra vagabundeando por el Bosque del Olvido, donde es incapaz de recordar qué día de la semana es. En el bosque viven el León y el Unicornio. El León miente los lunes, martes y miércoles. El Unicornio miente los jueves, viernes y sábados. En todas las demás ocasiones, ambos personajes dicen siempre la verdad. Alicia les pregunta y el León dice: "ayer me tocó mentir", mientras que el Unicornio asegura: "a mí también me tocó mentir ayer". ¿Qué día de la semana es hoy?
Segundo misterio: el retrato de Porcia
Porcia, la protagonista de El mercader de Venecia, presenta a sus pretendientes tres cofres, cada uno con una inscripción. En uno de ellos se encuentra su retrato y quien lo descubra podrá casarse con la bella joven. Porcia (quien siempre dice la verdad) asegura que a lo sumo una de las tres inscripciones es verdadera. Las inscripciones de los tres cofres pueden verse en el dibujo, ¿en cuál de ellos se encuentra el retrato de Porcia?

Tercer misterio: la Isla de los Zombis
En la Isla de los Zombis, junto a los humanos, que siempre dicen la verdad, conviven los zombis, que siempre mienten, aunque no se pueden distinguir externamente de los humanos. Para complicar, la cosa, en el idioma de la isla, las preguntas que normalmente se contestarían con un "sí" o un "no" se responden con las palabras "bal" o "da", pero el visitante no sabe cuál significa "sí" ni cuál significa "no".
Se proponen dos enigmas: supongamos que preguntamos a un lugareño si "bal" significa "sí" y que éste responde: "bal"; no podemos saber lo que significa "bal", pero ¿podremos saber si le hemos preguntado a un zombi o a un humano?
El otro enigma es algo más complicado, ¿es posible plantear una única pregunta, cuya respuesta sea "bal" o "da", que nos permita saber qué significa "bal"?
Cuarto misterio: vampiros de Transilvania
En Transilvania conviven humanos, que siempre dicen la verdad, y vampiros, que siempre mienten. Sin embargo, para complicar un poco la cosa, la mitad de los habitantes, ya sean humanos o vampiros, están locos. Así, hay cuatro tipos de habitantes en Transilvania: humanos cuerdos, humanos locos, vampiros cuerdos y vampiros locos.
Un individuo loco cree que todas las afirmaciones ciertas son falsas y que todas las afirmaciones falsas son verdaderas. Gracias, a Dios, todos los habitantes de Transilvania hablan español y contestan con un "sí" o un "no".
¿Se podría saber, mediante una única pregunta, si un transilvano al que le preguntamos es un vampiro? y ¿se podría saber, también mediante una única pregunta, si la persona a quién interrogamos está loca?
Anécdotas lógicas
Pasamos a ver unas anécdotas lógicas que le han podido suceder a cualquiera o casos similares. Estas anécdotas son fáciles de recordar y son interesantes ya que cualquier día uno se puede encontrar con algo parecido.
1. Un día de los inocentes, estaba Raymond enfermo en cama. Por la mañana, su hermano (diez años mayor que él) vino a su habitación y dijo: “Bien, Raymond, hoy es el día de los inocentes, y ¡te voy a hacer una broma como nunca te han hecho antes!”. Raymond espero todo el día que le hiciera una broma, pero su hermano no hizo nada.
Raymond estuvo despierto hasta mucho después de apagar las luces, tratando de determinar si le había hecho, su hermano, una broma o no. ¿Hubo inocentada o no?
Este acertijo o anécdota crea un tema de debate bastante lógico, valga la redundancia, probad a contárselo a cierto grupo de personas, a ver que opinan.
2. Un compañero de Raymond, de la Universidad de Chicago, tenía dos hermanos, uno de seis y otro de ocho años. Raymond iba frecuentemente por su casa y les hacía juegos de magia a los niños. Un día llegó y los dijo: “Tengo un truco con el que puedo convertiros a los dos en leones.”. Con gran sorpresa por su parte, uno de ellos saltó: “Vale, conviértenos en leones.” “Bueno, es que, la verdad, es que… bueno, no lo puedo hacer porque luego no podría volveros a convertir en niños.” Pero el pequeño contesto: “Qué más da, quiero que nos conviertas en leones de todas formas.” “No, de verdad que no hay ninguna forma de desconvertiros después.” El mayor gritó: “¡Quiero que nos conviertas en leones!” A la vez que el pequeño preguntaba: ¿Y cómo haces para convertirnos en leones?” “Ah, pues pronunciando las palabras mágicas” “¿Y cuáles son? Dínoslas” “Para decirlas tendría que pronunciarlas y entonces os convertiríais en leones” Se quedaron pensando un momento y luego uno de ellos preguntó: “Pero, ¿no hay otras palabras mágicas para desconvertir?” “Si, claro que las hay, lo que pasa es que si digo las primeras palabras mágicas os convertiríais en leones, pero no solo vosotros sino todo el mundo, incluido yo, y como los leones no saben hablar, no quedaría nadie en el mundo que pudiera decir las otras palabras mágicas para desconvertirnos.” El mayor dijo rápidamente: “Pues escríbelas.” Pero el pequeño dijo: “Jo, yo no se leer.” “No, no, lo de escribirlas es totalmente imposible, porque incluso escritas convertirían a todo el mundo en león.” Miraron a Raymond y dijeron: “Ah”.
Una semana después se encontraron Raymond y el niño de ocho años, este le dijo: “Raymond, ¿sabes qué? Quiero preguntarte una cosa que estoy pensando desde hace mucho tiempo.” “¿El qué?” Le dije. “Oye, ¿Y cómo hiciste tu para aprender las palabras mágicas?”
Muchas veces los niños nos hacen darnos cuenta de que no somos todo lo listos que parecemos y que incluso ellos nos pueden ganar una batalla intelectual si se lo proponen. ¿Cuantas veces nos hemos visto sorprendidos por preguntas impertinentes o no de unos niños? Nunca nos dejarán de llamar la atención, porque cada persona ve el mundo a su manera y reacciona con su lógica. En este caso, está claro que niños y mayores tienen puntos de vista distintos y utilizan la lógica de la manera con la que ellos creen que podrán resolver los problemas.
3. El otro día nos preguntaron de qué signo éramos. A la manera de Smullyan, contestamos: -Los de Escorpio y Capricornio no creemos en la astrología. ¿Lo pilláis? Pensad un poco y os saldrán unas cuantas paradojas de la vida diaria.
Caracterizaciones de la lógica
La lógica se puede caracterizar, usándola de la forma que más nos interese o convenga, esto nos puede convertir en unos pillos o espabilados según qué situación.
1. Una vez vi este chiste en un periódico: un niño y una niña van andando por una acera. El niño va por la parte de dentro. Pasa un camión por la calle, que está toda embarrada y pone perdida a la niña. El niño la mira y le dice: “¿Te das cuenta ahora por qué yo no voy por el lado de fuera como un caballero?”
Es lógico por una parte que el niño actúe así por su bien y demuestre a la niña su sinceridad, aunque siempre hay que intentar ser un caballero, el hombre es un animal egoísta que suele mirar primero por él. Y gracias a que la niña obvia la lógica acaba embarrada.
2. También me gusta esta caracterización de la ética. Un niño le pregunta a su padre: Papá, ¿Qué es la ética? Te lo voy a explicar, hijo mío. El otro día entré una señora en la tienda y me dio un billete de 5000 creyendo que era de 1000. Yo tampoco me di cuenta y le di la vuelta de las 1000. Horas después vi allí el billete y me di cuenta de lo que había pasado. La ética, hijo mío, es el preguntarme: “¿Tengo que decírselo a mi compañero (y repartir)?”
Este es un buen chiste de lógica para explicar que uno se puede aprovechar de los demás pero irónicamente no es nada ético el final de la situación.
3. Un día fui a un restaurante chino con un amigo que es matemático. El menú tenía una advertencia que decir: Precio extra por todo servicio extra. Mi amigo señaló: “Realmente, podrían haber quietado la segunda y la última palabra”.
Sobre todo en publicidad, en mercados, en ofertas es fácil encontrarse son este tipo de frases o títulos que realmente no dicen o expresan nada, pero que son capaces, muchas veces, de engañar a la gente. Gracias a que alguna gente aplica la inteligencia y la lógica se dan cuenta del engaño de este tipo de enunciados.
4. Una vez vi el siguiente cartel en un restaurante:
La buena comida no es barata. La comida barata no es buena.
¿Estas dos oraciones dicen o no dicen lo mismo? La respuesta sería que, hablando lógicamente, dicen exactamente lo mismo; ambas son equivalentes al enunciado de que no hay comida a la vez buena y barata. Pero, aunque ambos enunciados son lógicamente equivalentes, psicológicamente sugieren cosas diferentes: al leer la primera frase, me imagino unos platos muy refinados y caros pero, cuando leo la segunda, lo primero que veo es una comida barata y podrida.
Ciertamente, las frases dice lo mismo, pero como comentábamos, anteriormente, estas son estrategias de publicidad para atraer al posible comprador hacia lo que el vendedor quiere.
¿Es usted físico o matemático?
¿Físico o matemático? Depende de cada persona, hay problemas que pueden resolverse de una manera u otra, aplicando un criterio u otro. Y, algunas veces, un criterio es mejor que otro y podemos sacarle partido a la situación.
1. Hay un problema muy famoso sobre 2 garrafas que una tiene 10 litros de agua y la otra 10 litros de vino. Se echa tres litros de agua en la garrafa del vino y, tras resolverlo todo, se vuelven a echar 3 litros de de la mezcla en el recipiente del agua. Después de los trasiegos, ¿Qué habrá, mas agua en la garrafa del vino o más vino en la garrafa del agua?
Hay 2 maneras de resolver el problema, una aritmética y otra de sentido común. De las 2 prefiero como mucho la última.
La solución por el método aritmético es la siguiente: Después de echados 3 litros de agua en el recipiente del vio, tendremos en este 13 litros de mezcla consistente en 3/13 litros de agua y 10/13 litros de vino. Tras echar 3 litros de la mezcla de vuelta en la garrafa del agua, habré echado 3 x 10/13=30/13 litros de vino al agua. De forma que el recipiente de agua tendrá ahora 30/13 litros de vino. Ahora, antes del segundo trasiego, la garrafa del vino contendrá 3 litros de agua, y de la mezcla, se había devuelto al recipiente del agua 3 x 3/13. Así pues, la garrafa del vino tiene ahora 3 – 9/13 litros; pero 3 – 913=39/13 – p/13 = 30/13, de manera que la garrafa del vino tiene exactamente la misma cantidad (30/13) de agua que la garrafa de agua tiene de vino.
La solución por el método del sentido común es mucho más rápido y, también, nos hace pensar en algo mucho mas rápida, y también nos hace pensar en algo mucho más general: Dado que las cantidades de líquido de ambos recipientes sigue siendo la mismo, es evidente que cualquiera que sea el agua que falta de la garrafa del agua, ha sido reemplazada por el mismo volumen de vino. Y con esto se resuelve el problema. Evidentemente, esta solución de sentido común no te da el volumen, mientras que la solución aritmética te dice que es 30/13, tras que la solución aritmética te dice que es 30/13. Pero, en cambio, la solución tiene sentido común se puede aplicar igualmente al siguiente problema más general (que el método aritmético no puede resolver).
Para empezar, tenemos 2 recipientes que antes y echamos el liquido del uno en el otro repetidas veces sin especificar cuantas veces ni qué cantidad de líquido, ni tampoco es necesario que se eche la misma cantidad cada vez pero, terminando los trasiegos, tendremos 10 litros en cada recipiente. ¿Qué habrá, más agua en el del vino o más vino en el del agua? Por el mismo razonamiento de sentido común, las cantidades tendrán que ser las mismas, pero ahora sí que no podremos saber el volumen exacto.
A veces, el sentido común, el físico, es más potente que las propias matemáticas y nos puede ayudar a resolver problemas de hoy en día. La ciencia nunca deja de sorprendernos.
2. Este problema se puede resolver por el método difícil o por el fácil. Dos trenes, que van en la misma dirección y sentido contrario, están a 100 km el uno del otro; los dos andan a 50 km por hora. Una mosca empieza a volar del uno al otro, empezando por la parte delantera de uno de ellos, a una velocidad de 75 km a la hora. Los trenes chocan y la mosca muere aplastada ¿Cuántos kilómetros de vuelo hizo?
La mosca tocará cada tren un número infinito de veces antes de que la aplasten, y el problema se podría resolver sumando una serie infinita de distancia (cada vez más cortas, claro está, que convergen en una cantidad finita determinada), siendo este el método difícil y habría que hacerlo con papel y lápiz. El camino fácil seria el siguiente: si los trenes van a 50km/hora, los trenes tardarán en chocar dos horas, y, por tanto, la mosca habrá estado volando dos horas; como volaba a 75km/hora, habrá volado 150 kilómetros, y ya lo hemos resuelto.
El gran matemático Von Neumann le dieron este problema, pensó unos segundos y dijo: 150 kilómetros y le preguntaron cómo lo hizo y dijo: “Sumé la serie”.
Von Neumann resolvió el problema por sentido común pero “engaño” a la gente y fomentó su fama de matemático aprovechándose de esta situación. ¡Eso si que es inteligencia!
Gentes de Vermont
Veamos unos chistes o acertijos de las gentes de Vermont. Vermont es un estado de los Estados Unidos de América. Esto será similar a como nos mofamos con los habitantes de Lepe, aquí en España.
1. Me he acordado de lo que se contaba de Calvin Coolidge cuando fue de visita a una granja con unos amigos. Estando allí vieron un rebaño de ovejas y uno de los amigos dijo: “Se ve que acaban de esquilar a las ovejas”. “De este lado parece que si, comentó Coolidge”.
Parece lógico que si uno ve una oveja desde un lado y está esquilada, supuestamente está esquilada entera, pero claro, por que lo consideramos lo normal, que no lo lógico. No nos confundamos, porque perfectamente podrían estar, como opinaba el amigo Coolidge, esquiladas por un lado y habría que ver si del otro lado también las esquilaron para verificar si las esquilaron enteras.
2. Típico de los de Vermont, o por lo menos de cómo los pintan en los chistes, es que cuando se les pegunta por algo, contestan con toda precisión, pero casi siempre se les olvidad decir lo mas importante, como por ejemplo en este chiste: un granjero de Vermont va a la granja de su vecino y le pregunta: “Lem, ¿Qué le dijiste al caballo el año pasado cuando tuvo el cólico?” “Salvado y melaza”. El granjero se fue a su casa y una semana después volvió a ver a su vecino: “Lem, le di salvado y melaza a mi caballo y se me murió.” “Lo mismo que el mío.”
Muchas veces damos cosas por hechas cuando nos las dicen, pero los lenguajes a veces son tan complejos que si no hacemos más preguntas podemos dar por hecho cosas que no son ciertas. Nunca os quedéis sin preguntar algo que no sepáis. Preguntando se obtienen más verdades que callando.
Computadores
Aprovechando que los posibles lectores de este documento puedan ser gente relacionada con la informática y también, la implantación de las nuevas tecnologías en la vida diaria, vamos con uno de ordenadores.
Hay un chiste de un vendedor de IBM que quería vender un computador que lo sabía todo; le dijo a un cliente: “Pregúntele lo que quiera, que se le contestará.” “Vale, ¿Dónde está mi padre?” La máquina pensó unos instantes y le salió una tarjeta que decía: “Su padre está pescando en Canadá”. “Já.” dijo el cliente, “esta máquina no vale para nada, mi padre se ha muerto hace unos años.” A lo que el vendedor replicó que había que hacerle las preguntas en un lenguaje más preciso y, acercándose al computador le preguntó: “Este hombre está delante de ti, ¿Dónde está el marido de su madre?” El computador pensó un momento y le salió otra tarjeta: “El marido de su madre murió hace años.” “Su padre está ahora pescando en Canadá.”
Este chiste nos deja casi sin palabras. Nos muestra, de una manera un poco exagerada, que los computadores, a veces, son más listos que el ser humano y nos da toda una lección.
Monerías
Las monerías son demostraciones curiosas, que para el lector poco inteligente y sin sentido del humor, pueden parecer chorradas, pero para el que sabe apreciar la lógica, se divertirá un rato. Dentro de este apartado se consideran los silogismos, que son una forma de razonamiento lógico, que a la par pueden ser graciosos y que estamos hartos de ver.
1. Un filósofo se asombró cuando Rusell le dijo que una proposición falsa implica cualquier proposición. Le dijo: “¿Quieres decir que del enunciado de que dos más dos es igual a 5 sigue que tu eres el Papa?” Russell respondió: “Si.” El filósofo preguntó: “¿Puedes demostrar esto?” Russell respondió: “Ciertamente”, e inventó en el acto la demostración siguiente:
1) Supón que 2 + 2 = 5
2) Sustrayendo dos de ambos lados de la ecuación obtenemos 2=3
3) Transponiendo, obtenemos 3=2
4) Sustrayendo uno de ambos lados, obtenemos 2=1.
Ahora bien, el Para y yo somos dos. Puesto que dos es igual a uno, entonces el Papa y yo somos uno. Por consiguiente yo soy el Papa.
Esto es una demostración en toda regla, ya que a base de proposiciones verdaderas se van sacando conclusiones, encadenando estas se llega a un razonamiento lógico bastante curioso.
2. ¿Qué es mejor, la felicidad eterna o un bocadillo de jamón? Podría parecer que la felicidad eterna es mejor, ¡pero esto no es realmente así! Después de todo, nada es mejor que la felicidad eterna, y un bocadillo de jamón es ciertamente mejor que nada. Por lo tanto un bocadillo de jamón es mejor que la felicidad eterna.
Se vuelve a demostrar otra cosa con este silogismo. Ya sabemos que la felicidad eterna sería lo mejor ¿no? Pero nosotros planteamos otra cuestión. Si tienes muchísima hambre ¿qué prefieres, el bocata o la felicidad? Juzguen ustedes mismos.
3. Lo que sigue se debe a Lewis Carroll. ¿Que es mejor, un reloj que se atrasa un minuto cada día o un reloj que no funciona en absoluto?
La solución que puede parecer correcta sería el que se atrasa pero no es del todo cierto, ya que no nos marca ninguna hora bien y el reloj que no funciona, al menos 2 veces al día nos da la hora correcta. ¿Qué os parece esta solución?
Veamos lo que decía Lewis Carroll.
El reloj que no funciona en absoluto es mejor puesto que marca la hora exacta dos veces al día, mientras que el otro marca la hora exacta una vez cada dos años. “Pero,” podrías preguntar “¿de qué sirve que marque la hora exacta dos veces al día si no puede decirse cuando llega la hora?” Bien, supón que el reloj señala las ocho en punto. Entonces cuando dan las ocho el reloj marca la hora exacta. “Pero”, continúas, “¿cómo sabes cuando son las ocho en punto?” La respuesta es muy simple. Todo lo que tienes que hacer es mantener muy cuidadosamente los ojos fijos en el reloj y en el preciso momento que tengan que ser serán las ocho en punto.
4. Esta es la mejor monería que conozco. Se trata de un método absolutamente inexpugnable para demostrar cualquier cosa Su único inconveniente es que solamente un mago puede presentarlo. He aquí lo que hago. Supóngase que quiero demostrar a alguien que yo soy Drácula. Digo: “La única lógica que usted ha de conocer es que, dados cualesquiera dos proposiciones p y q, si p es verdadera, entonces al menos una de las dos proposiciones p, q es verdadera.” Todo el mundo asentirá virtualmente a esto. “Muy bien”, digo mientras saco un mazo de cartas de mi bolso, “como usted puede ver esta carta es roja.”
A continuación coloco la carta roja boca abajo en la palma de la mano izquierda de la victima y le hago cubrir el dorso de la carta con su mano derecha. Continúo: “Sea p la proposición de que la carta que usted tiene es roja; sea q la proposición de que yo soy Drácula. Puesto que p es verdadera, ¿admite usted que o p o q es verdadera?” Él asiente. “Bien, ahora”, continúo yo, “p es obviamente falsa; dé la vuelta a la carta.” Él lo hace y, ante su sorpresa la carta es negra! “Por consiguiente”, concluyo, “q es verdadera, de modo que yo soy Drácula.”
Curiosa demostración lógica en un formato mágico la que nos plantea Smullyan. Pero aún nos quedaría una pregunta por resolver, ¿Cómo cambio la carta, que estaba en la mano del espectador, de color?
Otros enigmas matemáticos
Cómo colofón final, planteamos otros enigmas matemáticos para abrir las mentes de los lectores. Posiblemente los habréis visto en otros sitios, si es así a ver si os acordáis de su solución, ni nunca lo visteis, adelante, a por ellos.
1. ¿Qué orden siguen los siguientes números?
4 – 5 – 2 – 9 – 8 – 6 – 7 – 3 – 1 .
2. Un pastelero recibe tres cajas opacas, Una caja contiene caramelos de menta, otra caramelos de anís y la otra un surtido de caramelos de menta y anís. Las cajas están etiquetadas de la siguiente manera:

El pastelero recibe el aviso de que todas las cajas están mal etiquetadas. ¿Cuántos caramelos tendrá que sacar el pastelero, como mínimo, para verificar el contenido de las cajas?
3. En el interior de una habitación, herméticamente cerrada, hay una bombilla. Fuera de la habitación hay tres interruptores. Sólo uno de los tres enciende la bombilla. Mientras la puerta este cerrada, puedes pulsar los interruptores las veces que quieras, pero al abrir la puerta hay que decir cual de los tres interruptores es el que enciende la bombilla. ¿Cómo averiguaríamos cual es el interruptor que enciende la bombilla?
4. Un alumno le pregunta a un profesor, “¿Qué edad tienen tus tres hijas?” y el profesor contesta, “si multiplicas sus edades da treinta y seis, y si las sumas da el número de tu portal de casa”, “me falta un dato”, protesta el alumno, y el profesor le responde “ah, es verdad, la mayor toca el piano”. ¿Qué edad tienen las tres hijas?
Otro problema de ajedrez retrospectivo
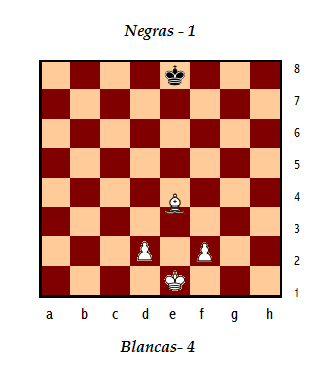
A continuación uno procedente de uno de los libros más populares sobre el tema: “Juegos y problemas de ajedrez para Sherlock Holmes”, de Raymond Smullyan. Éste me gusta especialmente por su mezcla de sencillez y complejidad: no requiere realizar largos razonamientos lógicos, en realidad sólo requiere uno, pero quizá más intuitivo que en la mayoría de los casos, es decir, no hay que recorrer muchos y largos caminos, pero hay que dar un salto bastante grande para llegar a la meta. Dice así:
En esta partida ninguna pieza movió de una casilla blanca a una negra y viceversa. En qué casilla está el alfil blanco, ¿en la e3 o en la e4?
¿En qué casilla se sitúa el alfil?
Si después de un rato no se te ocurre nada siempre puedes echar una ojeada a la pista, pero cuidado, porque igual te desconcierta más que te ayuda:
Pista.- Se podría quitar el alfil del tablero y exponer el problema de la siguiente manera, siendo el razonamiento análogo: En esta partida ninguna pieza movió de una casilla blanca a una negra y viceversa. Existe otra pieza en el tablero. Esa pieza, ¿está en una casilla blanca o negra?
Conclusiones
Todos los acertijos sin resolver, planteados en este documento, tienen solución, sólo hay que estrujarse un poco el cerebro. Si aún así no sois capaces de encontrar la solución, podéis encontrar las mismas dentro del contenido de “Bibliografía y material consultado”.
Bibliografía y material consultado
Libro: “¿Cómo se llama este libro?” de Raymond Smullyan.
Libro: “¿La dama o el tigre?” de Raymond Smullyan.
Libro: “Juegos y Problemas de Ajedrez para Sherlock Holmes” Raymond Smullyan
Película: “La habitación de Fermat” de Luis Piedrahita y Rodrigo Sopeña.
Enlace: http://es.wikipedia.org/wiki/Raymond_Smullyan
Enlace: http://es.wikipedia.org/wiki/L%C3%B3gica
Enlace: http://es.wikipedia.org/wiki/Vermont
Enlace: http://es.wikipedia.org/wiki/Silogismo
Enlace: http://bucles.wordpress.com/category/logica/
Enlace: http://boards5.melodysoft.com/app?ID=canalingenio&msg=374&DOC=51
Enlace: http://www.arrakis.es/~owenwang/articulos/pasatiempos.htm
Enlace: http://patatitaspochas.blogspot.com/2007/09/cmo-se-llama-esta-entrada.html
Enlace Lemuel (2007) Lógica coactiva. http://boards5.melodysoft.com/app?ID=canalingenio&msg=374&DOC=51
Fuente: http://campusvirtual.unex.es/cala/epistemowikia/index.php?title=Raymond_Smullyan_y_problemas_de_l%C3%B3gica#An.C3.A9cdotas_l.C3.B3gicas